Six Jumping Frogs and
the Aesthetics of Problem Solving
Download as PDF file

Lee Humphries

Last week my friend Jack emailed me a puzzle.  Chinese second-graders are said to solve it in two minutes.  I mustered my courage and gave it a try.  (You need not work the puzzle to understand this article.  But if you want to have a go at it, there’s an automated Excel version at this link.) 

The puzzle involves seven rocks and six frogs.  See Fig. 1.  The seven rocks are laid out in a horizontal line and numbered left to right.  The six frogs are evenly divided into a green trio and a brown trio.  The green frogs sit on Rocks 1, 2, and 3, facing right.  The brown frogs sit on Rocks 5, 6, and 7, facing left.  Rock 4 is vacant. 

The challenge is to transpose the trios, jumping the green frogs to Rocks 5, 6, and 7 and the brown frogs to Rocks 1, 2, and 3.  Their movement is restricted.  A frog can only jump forward, either hopping to a vacant rock one place ahead or leaping over its neighbor frog to a vacant rock two places ahead.

Fig. 1. Seven rocks and six frogs

Let me report that I would be a dismal second grader in the People's Republic of China and probably in most other countries as well.  Prodding six frogs to opposing destinations along a one-lane road of seven rocks took me far longer than two minutes.  And once my frogs arrived, I couldn’t remember the sequence of jumps that got them there.  To rediscover it, I had to start over.  The frogs’ second coming was as protracted as their first.  Could I have done better?

Remembrance of Things Past

Having no idea what pattern underlay the solution, I began with my only option—spontaneous action.  I jumped my frogs by impulse, observed the result, and tried to get a feel for the situation.  For meaningful problems, I keep a running log of what I'm doing and thinking—a substitute for my unreliable memory.  But the frog puzzle was a momentary diversion, so I didn’t bother to record my jumps.  That was a mistake: Lacking a catalog of failed strategies as a reference, I wasted time retracing previously unsuccessful paths. 

Eventually, certain jump sequences, repeated ad nauseam, stuck in my brain.  Recalling them, I eliminated the wrong ones and conjoined the right ones.   Before my memory faded again, I recorded the entire sequence of fifteen correct jumps—not in a list, but in a diagram.  See Fig. 2.

 Fig. 2.  The correct jump sequence

A diagram of the jumps has a coherence that a list of the jumps lacks.  Viewable at a glance, it presents the complete data set all-at-once, integrating the many jumps into a single visual gestalt.  With the total configuration in plain sight, there is nothing to recall; the demand on short-term memory is negligible.

A list, on the other hand, must be processed incrementally via many disconnected eye shifts.  The totality can only unfold bit-by-bit as one reads through the items—and can’t be completely known until all items are pieced together in short-term memory.  So, a list is a memory-intensive presentation.   If a list’s length exceeds the memory’s channel capacity, items will be forgotten, leaving an incomplete data set from which to infer the shape of the whole.

Depth of Understanding

Even though the puzzle’s solution—finally recovered and diagrammed—was behind me, my understanding of it was shallow.   I only knew the jump sequence itself (and its mirror image, which also solves the puzzle).

I wondered if the sequence followed some pattern.  Should a pattern exist, anyone who knew it—say, a Chinese second-grader—could implement it and quickly solve the puzzle.   Knowing this pattern, one would have a deeper understanding of the solution.

And what if that pattern derived from some general organizing principle that underlies the solutions to many puzzles; puzzles different in their particulars but alike in their form?  Knowing the principle, one would have a very deep understanding of the solution; one could easily solve sundry puzzles (and seem a miracle worker to naive onlookers).

I examined the solution for patterns, looking for one that governed the jump sequence.  There were several of interest.

Beautiful Deceivers

The aesthetic appeal of certain patterns is entrancing; attention gravitates to them.  But sometimes they are secondary—mere byproducts of a primary, generative pattern.  Attractive though trivial, they can blind us to truly significant patterns.  Descriptions of secondary patterns, however accurate, don’t explain the underlying process that produced them. 

Here are four kinds of patterns present in the puzzle’s solution:

·         the ordinal pattern in which the six uniquely numbered frogs jump

·         the color pattern in the jump sequence

·         the directional pattern in the jump sequence

·         the hop-leap pattern in the jump sequence

These patterns were found to be secondary—but only after their beguiling beauty enticed me down some blind alleys.  What were their attractions (and their failings)?

Blind Alley # 1: The ordinal pattern in which six uniquely numbered frogs jump.  The successful solution requires the frogs to jump in the order shown below.  (Each frog bears the number of the rock on which it first sits.  There is no Frog 4 because Rock 4 is initially vacant.  Frog 3 makes the first jump; Frog 5, the second; etc.)

3    5    6    3    2    1    5    6    7    3    2    1    6    7    1

The longest recurring jump pattern involves Frogs 3, 2, and 1 (in that order).  It appears twice—in symmetrically balanced locations.  The symmetry is appealing.

3    5    6    3    2    1    5    6    7    3    2    1    6    7    1

There are two shorter recurring patterns.  One involves Frogs 5 and 6; the other, Frogs 6 and  7.  Each pattern appears twice.

3    5    6    3    2    1    5    6    7    3    2    1    6    7    1

3    5    6    3    2    1    5    6    7    3    2    1    6    7    1

One might claim that the two shorter patterns are partnered since they dovetail in the three central jumps and counterbalance each other near the extremes.

3    5    6    3    2    1    5    6    7    3    2    1    6    7    1

Despite all this, there is no systematic process unfolding across the entire jump sequence.  (Changing the numbers assigned to the frogs won’t change the abstract forms of the internal patterns, which are a property of the jump sequence itself.)

Blind Alley # 2: The color pattern in the jump sequence.  Frogs 1, 2, and 3 are green (G).  Frogs 5, 6, and 7 are brown (B).  Thus, the successful jump sequence produces this color pattern:

The first six jumps neatly reduce to alternating groups of green and brown frogs; each successive group adds one more frog.  We might extrapolate from the process observed in Groups 1 through 3, inferring that Group 4 will have four brown frogs.  We would be right about the color but wrong about the number: The fourth group fails to add a fourth brown frog.  The process dies out.

The complete color pattern has a simplicity lacking in the complete number pattern.  It is a palindrome—it reads the same forward and backward.  But prior knowledge that the solution is palindromic won’t unravel the puzzle; we need specifics.

In truth, even if we were told the complete color pattern, our success would not be assured.  The pattern can’t reveal which green or brown frog jumps.  Sometimes there are two possibilities.

Blind Alley # 3: The directional pattern in the jump sequence.  Because green frogs move right (R) and brown frogs move left (L), the solution’s directional pattern is equivalent to its color pattern.  The two patterns are different expressions of the same information; therefore, both have the same structure and the same shortcomings.

Blind Alley # 4: The hop-leap pattern (one place or two) in the jump sequence.  Like the color pattern and the directional pattern, the hop-leap pattern is a palindrome.

1    2    1    2    2    1    2    2    2    1    2    2    1    2    1

It also contains a “1-2” progression in which the number of twos systematically increases and decreases.

1    2    1    2    2    1    2    2    2    1    2    2    1    2    1

This pattern looks more promising.  Its process encompasses the entire sequence of jumps—provided we think of the sixth pattern as having zero twos.  But, alas, it too cannot specify which frog jumps—and occasionally there are two contenders.

After flirting with these different patterns, I awoke one morning with the thought that I might be looking at things from the wrong perspective.   Normally, our attention is drawn to movement, not stillness.  The idea that the frogs were jumping had elevated them in my consciousness.  But maybe the matrix resided in what was still—the rocks from which the frogs jumped.  Maybe the background was really the foreground.  A Zen master would like this notion.

I applied my new perspective to the solution—still numbering the seven rocks from left to right.  The sequence of rocks from which my frogs successfully jumped was this.

3    5    6    4    2    1    3    5    7    6    4    2    3    5    4

(A frog’s destination is always known: It jumps to a vacant rock, and only one rock can be vacant at a time.)

I grouped the numbers in various ways, searching for a controlling pattern.  At first, nothing caught my eye.  Then without warning an Aha! jerked open my mental curtain, displaying in high illumination the solution’s organizing principle.

Description vs. Diagram

The principle described.  What I saw was a series of consecutive odd numbers ascending, a series of consecutive even numbers descending, and a repeated alternation between the two.

The numbers in each series were symmetrically positioned with respect to the central rock (Rock 4).  The initial series was the central rock’s two neighbors.  Then, alternately, each series added one rock until the series of odd numbers reached its maximum—spanning all seven rocks. 

Thereafter, the process reversed itself.  Alternately, each series subtracted one rock until the even-numbered series reached its minimum—containing only the central rock. 

The most beautiful pattern of all, I thought.

The problem with descriptions.  Despite my best effort to describe the solution’s organizing principle, many readers will arrive at this paragraph confused.  That’s because the principle is a gestalt, an all-at-once set of integrated relationships, whereas my description of it is a bit-by-bit presentation, likely to exceed the channel capacity of short-term memory.  A description that won’t fly with adults will surely crash with second-graders.

The principle seen.  Let’s try again, using another diagram, Fig. 3.  This visual representation of the solution conveys all-at-once the same information conveyed incrementally in “The principle described”—an integrated collection of numerical series (odd and even, ascending and descending, expanding and contracting, maximizing and minimizing, symmetrically arranged).

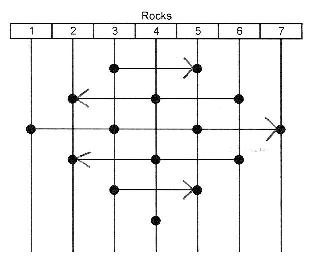
Fig. 3.  Solution to the six-frog puzzle:
The sequence of rocks from which frogs jump

The principle applied.  Anyone who looks at this diagram and sees through to the solution’s organizing principle should be able to apply the principle to a related puzzle, solving it in a single try.  To prove to myself that this is true, I set up two similar puzzles: one of five rocks and four frogs (two green and two brown, separated by a vacant rock), and another of nine rocks and eight frogs (four green and four brown, separated by a vacant rock).  In each puzzle I represented the green frogs with dimes, the brown frogs with pennies, and the vacant rock with a quarter.  When a frog jumped to the vacant rock, its coin and the quarter would trade places.

From the organizing principle observable in Fig. 3, I deduced two new patterns: a solution to the four-frog puzzle (Fig. 4) and a solution to the eight-frog puzzle (Fig. 5.) 

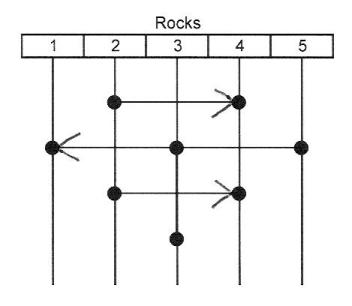
Fig. 4.  Solution to the four-frog puzzle:
The sequence of rocks from which frogs jump

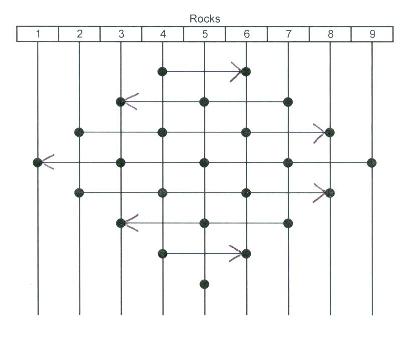
Fig. 5.  Solution to the eight-frog puzzle:
The sequence of rocks from which frogs jump

I applied the deduced patterns to their respective puzzles and solved both on the first attempt.

The speed at which a child completes a puzzle has less to do with some innate problem solving ability and more to do with the kinds of patterns s/he has previously encountered, manipulated, and internalized.   On-the-spot facility with a given problem requires prior cognitive experience with similar forms.  Or, lacking that, random good luck. 

Rightly, the highest mark for second-grade puzzle prowess should go to the kid who solves the frog problem in the greatest amount of time.  This would be a child who, lacking cognitive experience with its pattern class, drills down to the bedrock of understanding relying solely on observation, intuition, reasoning, and continuity of attention—a set of mental behaviors highly correlated with innovative breakthroughs.

A Musical Addendum

The solution to any frog puzzle can be represented by a melody in C major. Middle C stands for the middle rock. Notes above and below middle C stand for rocks located correspondingly right and left of the middle rock.

As mentioned earlier, each puzzle has two solutions, which are mirror images of each other. The melodies that represent the two solutions are, therefore, inversions of each other, centered on middle C. The melody in Fig. 6 represents the six-frog solution shown in Fig. 3.

Fig. 6. Six-frog solution represented as a melody

The melody in Fig. 7 is the inversion of the melody in Fig. 6. It represents the mirror image of Fig. 3

Fig.7. Six-frog solution's mirror image represented as a melody

©2007 ThinkingApplied.com